ICPC沈阳网络赛D. Fish eating fruit

发表于 | 阅读数

题意：

给一棵树,求两两距离%3为0,1,2的各个距离和。

比赛时由于沉迷于边分治，想转移想到自闭。最后被提醒用点的分治的方法做。就想转移方程真的恶心。
可以想到$O(n^2)$就是对每个点进行搜索。
那么对于一个点的搜索应该是

这样只能处理一个节点所贡献的值，尝试转移。

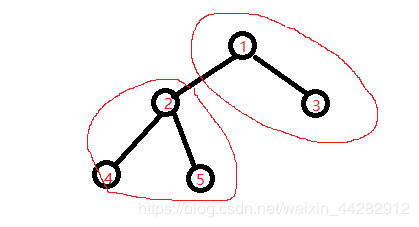
shanghaiC.png
假设已知$dis[1][j]$和$num[1][j]$求$dis[2][j]$和$num[2][j]$
那么先求$2$的爸爸$1$去掉$2$这条路之后的$dis[],num[]$
根据之前的式子，其实就是反过来。

那此时问题又变得简单了，就是将$1$这个儿子添到$2$上

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
const int M = 1e5 + 10;
const int mod = 1e9 + 7;
struct node
{
    int y, z;
} e;
vector<node> g[N];
int n;
ll num[N][3], dis[N][3], ans[N];
void addedge(int x, int y, int z)
{
    e.y = y;
    e.z = z;
    g[x].push_back(e);
}

void dfs1(int x, int f)
{
   
    num[x][0]++;
    for (int i = 0; i < g[x].size(); i++)
        if (g[x][i].y != f)
        {
            int son = g[x][i].y;
            int w = g[x][i].z;
            dfs1(son, x);
            for (int j = 0; j < 3; j++)
            {
                dis[x][(w + j) % 3] = (dis[x][(w + j) % 3] + w * num[son][j] % mod + dis[son][j]) % mod;
                num[x][(w + j) % 3] += num[son][j];
            }
        }
}
void dfs2(int x, int f)
{
    int di[3], nu[3], fan[3], fad[3];
    for (int i = 0; i < g[x].size(); i++)
        if (g[x][i].y != f)
        {
            int son = g[x][i].y;
            int w = g[x][i].z;
            for (int j = 0; j < 3; j++)
            {
                di[(w + j) % 3] = (dis[x][(w + j) % 3] - 1ll * w * num[son][j] % mod - dis[son][j] + 2 * mod) % mod;
                nu[(w + j) % 3] = num[x][(w + j) % 3] - num[son][j];
            }
            for (int j = 0; j < 3; j++)
            {
                fad[(w + j) % 3] = (w * nu[j] % mod + di[j]) % mod;
                fan[(w + j) % 3] = nu[j];
            }
            for (int j = 0; j < 3; j++)
                dis[son][j] = (dis[son][j] + fad[j]) % mod, num[son][j] = num[son][j] + fan[j];
            dfs2(son, x);
        }
}
int main()
{
    while (~scanf("%d", &n))
    {
        for (int i = 1; i <= n; i++)
            g[i].clear();
        for (int i = 1; i <= n; i++)
            for (int j = 0; j < 3; j++)
                dis[i][j] = num[i][j] = ans[j] = 0;
        for (int i = 1; i < n; i++)
        {
            int x, y, z;
            scanf("%d%d%d", &x, &y, &z);
            x++;
            y++;
            addedge(x, y, z);
            addedge(y, x, z);
        }
        dfs1(1, 0);
        //cout<<num[1][2]<<endl;
        dfs2(1, 0);
        for (int i = 1; i <= n; i++)
            for (int j = 0; j < 3; j++)
                ans[j] = (ans[j] + dis[i][j]) % mod;
        printf("%lld %lld %lld\n", ans[0], ans[1], ans[2]);
    }
}