HDU6035 Colorful Tree

发表于 | 阅读数

题意

给一颗树，求一条路径的值是路径上点的种类数，求$n*(n-1)/2$条路径值的总和

容易想到分别每个种类的贡献，但是如图一个种类的贡献不好求。不如求所有路径不经过此种类点的路径数。
如图我们要求没经过红点的路径数

然后比赛中我陷入如何找联通块的无线死循环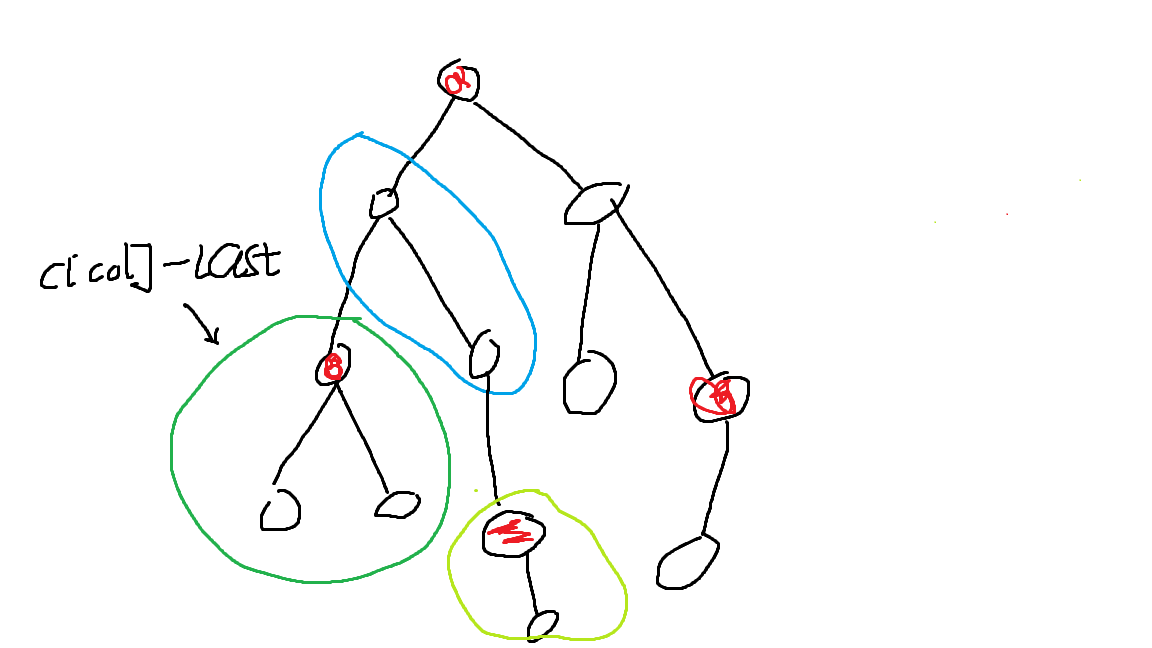
1.png

每当我们更新$c[color],通过c[color]-c[color]_{last}就可以知道c[u][color]$

然后为了减低空间复杂度，显然可以一边遍历一边更新$c[color]$，而做完一边所有儿子的的更新就要把自己也加到父亲的$c[color]$，最后要再总的统一一边

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <iostream>
#include <cstdio>
#include <cmath>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 2e6 + 10;
vector<int> g[N];

ll ans = 0;
int n, w[N], c[N], si[N], cnt, v[N];
void dfs(int x, int f)
{
    si[x] = 1;
    int col = w[x];
    int last = c[col];
    int els = c[col];
    //int y=c[col];
    for (int i = 0; i < g[x].size(); i++)
        if (g[x][i] != f)
        {
            int v = g[x][i];
            dfs(v, x);
            si[x] += si[v];
            int no = si[v] - (c[col] - last);
            ans -= 1ll * (no) * (no - 1) / 2;
            last = c[col];
        }
    c[col] = si[x] + els;
}
void init()
{
    ans = 0;
    cnt = 0;
    for (int i = 1; i <= n; i++)
        g[i].clear(), v[i] = c[i] = si[i] = 0;
}
int t = 0;
int main()
{
    while (~scanf("%d", &n))
    {
        t++;
        init();
        for (int i = 1; i <= n; i++)
            scanf("%d", &w[i]), v[w[i]] = 1;
        for (int i = 1; i < n; i++)
        {
            int u, v;
            scanf("%d%d", &u, &v);
            g[u].push_back(v);
            g[v].push_back(u);
        }
        dfs(1, 0);
        //cout<<ans<<endl;
        for (int i = 1; i <= n; i++)
            if (v[i])
                ans += 1ll * n * (n - 1) / 2 - 1ll * (n - c[i]) * (n - c[i] - 1) / 2;
        printf("Case #%d: %lld\n", t, ans);
    }
}