点分治

题意：
给出一棵树，求出树上距离不超过$k$的点对数量。

对于一棵子树，满足条件的路径包括(经过根的路径，和子树里的路径)!

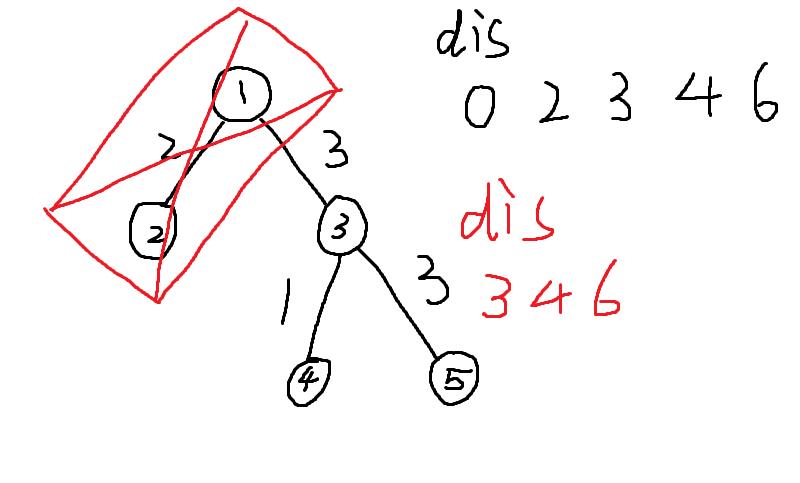
所以我先以它的根为起点，向下搜索，等到路途的$5$条路径长度$dis[5]$，假设$k=7$,通过$5$条路径的配对有$(2,3,4,5,6,7)$:

排序后，建立双指针$l=1,r=5$,若$a[l]+a[r]\leq k$则$(l,r]$里都成立。这样就只要$O(nlogn+n)$就可以实现找合理路径。

但是显然$(3+4)$这条路径不符合条件，它是$1->3->4与1->3$配对而成(因为我们需要不同一个子树里的路径互相配对),我们需要将他去掉，只需要在继续搜索子树结点时,再次使用以上方法找到子树的$3$条路径,在答案种减去符合的就好了。

但是为了退化到一条链的情况或是有个子树特别大：
假设当前树的重心为$u$,则整棵树的大小为$size(u)$,对于u的任意儿子v有，$size(v)<=size(u)/2$.
也就是说我们每次把重心删除以后，剩下的子树的规模都至少会是源树的一半。如果原来树的大小为$n$,那么递归的层数就会使$log(n)$

树的重心

模版

```c++ #include #include #include #include #include #include using namespace std; #define inf 0x7fffffff const int N = 1e5 + 10; struct node { int to, w, next; } e[N << 1]; int head[N], cnt, n, k, d[N], deep[N]; int num, ans, f[N], son[N], vis[N], root, sum; void addedge(int u, int v, int w) { e[++cnt].to = v; e[cnt].w = w; e[cnt].next = head[u]; head[u] = cnt; } void getroot(int x, int fa) { son[x] = 1; f[x] = 0; for (int i = head[x]; i; i = e[i].next) { if (e[i].to == fa || vis[e[i].to]) continue; getroot(e[i].to, x); son[x] += son[e[i].to]; f[x] = max(f[x], son[e[i].to]); } f[x] = max(f[x], sum - son[x]); if (f[x] < f[root]) root = x; } void getdeep(int x, int fa) { deep[++num] = d[x]; for (int i = head[x]; i; i = e[i].next) if (e[i].to != fa && !vis[e[i].to]) { d[e[i].to] = d[x] + e[i].w; getdeep(e[i].to, x); } } int calc(int x, int now) { int st = 0; d[x] = now; num = 0; getdeep(x, 0); sort(deep + 1, deep + 1 + num); int l = 1, r = num; while (l < r) { if (deep[l] + deep[r] <= k) st += r - l, l++; else r--; } return st; } void slove(int x) { ans += calc(x, 0); vis[x] = 1; for (int i = head[x]; i; i = e[i].next) if (!vis[e[i].to]) { ans -= calc(e[i].to, e[i].w); sum = son[e[i].to]; root = 0; getroot(e[i].to, root); slove(root); } } int main() { while (scanf("%d%d", &n, &k) != EOF && n && k) { ans = 0; root = 0; cnt = 0; sum = n; f[0] = inf; memset(vis, 0, sizeof(vis)); memset(head, 0, sizeof(head)); for (int i = 1; i < n; i++) { int u, v, w; scanf("%d%d%d", &u, &v, &w); addedge(u, v, w); addedge(v, u, w); } getroot(1, 0); slove(root); printf("%d\n", ans); } } ```

POJ 1655

树的重心

```c++ #include #include #include #include #include using namespace std; #define inf 0x7fffffff const int N = 2e5 + 10; struct node { int to, next, w; } e[N << 1]; int head[N], n, cnt, si[N]; int rootsiz, root; void init() { cnt = 0; memset(head, 0, sizeof(head)); root = inf; rootsiz = inf; } void addedge(int u, int v, int w) { e[++cnt].to = v; e[cnt].w = w; e[cnt].next = head[u]; head[u] = cnt; } void getroot(int x, int fa) { si[x] = 1; int tmp = 0; for (int i = head[x]; i; i = e[i].next) if (e[i].to != fa) { getroot(e[i].to, x); tmp = max(tmp, si[e[i].to]); si[x] += si[e[i].to]; } tmp = max(tmp, n - si[x]); if (tmp < rootsiz || (tmp == rootsiz && x < root)) { root = x; rootsiz = tmp; } } int T; int main() { scanf("%d", &T); while (T--) { init(); scanf("%d", &n); for (int i = 1; i < n; i++) { int u, v; scanf("%d%d", &u, &v); addedge(u, v, 1); addedge(v, u, 1); } getroot(1, 0); printf("%d %d\n", root, rootsiz); } } ```