树上启发式合并

发表于 | 阅读数

题意：
一棵树有$n$个结点，每个结点都是一种颜色$c_i\leq n$，每个颜色有一个编号，求树中每个子树的最多的颜色编号的和。

首先如果$ci$较小，就可以开一个二维数组$dp[N][M_c]$,将每个子树的状态记录下来，可惜空间不够和复杂度过高。但我们发现可以保留一些节点子树的状态，来降低复杂度，但是要保存那些呢？此时就要用到重儿子这个概念。

$Size[x]$:以$x$为根那颗子树的节点数
重儿子:一个根下,节点的$Size$最大
重链:根连接重儿子那条边
轻儿子:不是重儿子的儿子们
轻链:根连接轻儿子那条边
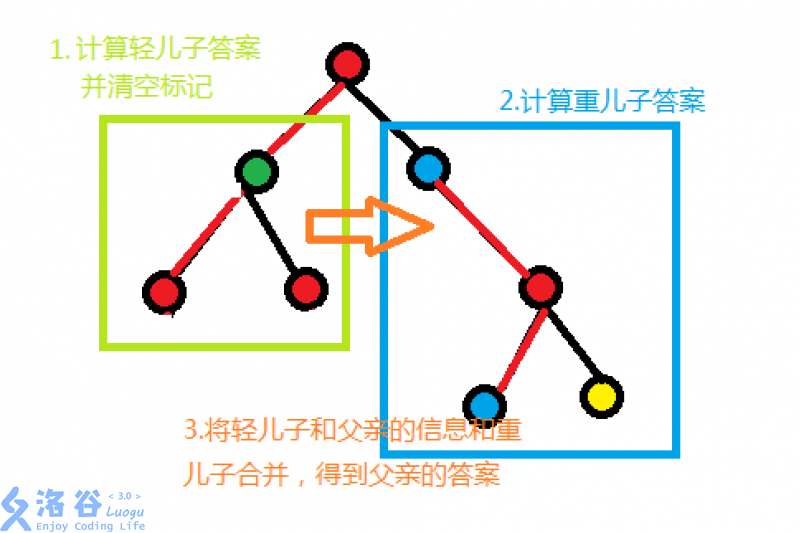
遍历一个节点，我们按以下的步骤进行遍历：

  • 先遍历其非重儿子，获取它的$ans$，但不保留遍历后它的状态
  • 遍历它的重儿子，保留它的状态
  • 再次遍历其非重儿子及其父亲，此时一条重链上的状态就会递归式完善，重链上的重儿子的状态对遍历到的节点进行计算，获取整棵子树的$ans$

根节点到树上任意节点的轻边数不超过$logn$条。我们设根到该节点有$x$条轻边该节点的子树大小为$y$，显然轻边连接的子节点的子树大小小于父亲的一半（若大于一半就不是轻边了），则$y<n/2^x,x<logn$。

又因为如果一个节点是其父亲的重儿子，则他的子树必定在他的兄弟之中最多，所以任意节点到根的路径一个一个走轻链($logn$)或者直接走重链(不会被重复计算+1)，所以一个节点的被遍历次数$=logn+1$,总时间复杂度则为 $O(n(logn+1))=O(nlogn)$

模板题$CF600E$

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 2e5 + 10;
const int mod = 1e9 + 7;
 
struct node
{
    int to, nxt;
} e[N << 1];
int head[N], cnt, n, w[N], son[N], siz[N];
int maxnum, num[N], vis[N];
ll ans[N];
ll res;
void addadge(int u, int v)
{
    e[++cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}
void predfs(int x, int fa)
{
    siz[x] = 1;
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if (v == fa)
            continue;
        predfs(v, x);
        siz[x] += siz[v];
        if (!son[x] || siz[son[x]] < siz[v])
            son[x] = v;
    }
}
void calc(int x, int fa, int flag)
{
    num[w[x]] += flag;
    if (flag > 0 && num[w[x]] > maxnum)
    {
        res = 0;
        maxnum = num[w[x]];
    }
    if (flag > 0 && num[w[x]] == maxnum)
        res += w[x];
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if (v == fa || vis[v] == 1)
            continue;
        calc(v, x, flag);
    }
}
void solve(int x, int fa, int flag)
{
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if (v == fa || v == son[x])
            continue;
        solve(v, x, 0);
    }
    if (son[x])
        solve(son[x], x, 1), vis[son[x]] = 1;
    calc(x, fa, 1);
    ans[x] = res;
    if (son[x])
        vis[son[x]] = 0;
    if (!flag)
        calc(x, fa, -1), res = 0, maxnum = 0;
}
int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", &w[i]);
    for (int i = 1; i < n; i++)
    {
        int u, v;
        scanf("%d%d", &u, &v);
        addadge(u, v);
        addadge(v, u);
    }
    predfs(1, -1);
    solve(1, -1, 0);
    for (int i = 1; i <= n; i++)
        printf("%lld ", ans[i]);
}

练手题$CF570D$

代码 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <queue>
#include <cmath>
#include <cstring>
#include <vector>
using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
const int mod = 1e9 + 7;

struct node
{
    int to, nxt;
} e[N << 1];
vector<pair<int, int> > q[N];
int head[N], cnt, n, son[N], siz[N];
int vis[N], dep[N], check[N];
char s[N];
int ans[N];
void addadge(int u, int v)
{
    e[++cnt].to = v;
    e[cnt].nxt = head[u];
    head[u] = cnt;
}
void predfs(int x, int fa, int d)
{
    dep[x] = d;
    siz[x] = 1;
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if (v == fa)
            continue;
        predfs(v, x, d + 1);
        siz[x] += siz[v];
        if (!son[x] || siz[son[x]] < siz[v])
            son[x] = v;
    }
}
int count(int x)
{
    int res = 0;
    while (x)
    {
        if (x & 1)
            res++;
        x /= 2;
    }
    return res;
}
void calc(int x, int fa, int flag)
{
    check[dep[x]] ^= (1 << (s[x] - 'a'));
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if (v == fa || vis[v] == 1)
            continue;
        calc(v, x, flag);
    }
}
void solve(int x, int fa, int flag)
{
    for (int i = head[x]; i; i = e[i].nxt)
    {
        int v = e[i].to;
        if (v == fa || v == son[x])
            continue;
        solve(v, x, 0);
    }
    if (son[x])
        solve(son[x], x, 1), vis[son[x]] = 1;
    calc(x, fa, 1);
    for (int i = 0; i < q[x].size(); i++)
    {
        int d = q[x][i].first;
        
        if (count(check[d]) <= 1)
            ans[q[x][i].second] = 1;
        else
            ans[q[x][i].second] = 0;
    }
    if (son[x])
        vis[son[x]] = 0;
    if (!flag)
        calc(x, fa, -1);
}
int m;
int main()
{
    scanf("%d%d", &n, &m);
    for (int i = 2; i <= n; i++)
    {
        int v;
        scanf("%d", &v);
        addadge(i, v);
        addadge(v, i);
    }
    scanf("%s", s + 1);
    for (int i = 1; i <= m; i++)
    {
        int v, h;
        scanf("%d%d", &v, &h);
        q[v].push_back(make_pair(h, i));
    }
    predfs(1,0,1);
    solve(1,0,0);
    for(int i=1;i<=m;i++)
    {
    	if(ans[i])
    		puts("Yes");
    	else
    		puts("No");
	}
}