KMP EXKMP MANNAR

发表于 | 阅读数

$KMP$:通过$next[]$,$T=$模式串与$S=$匹配串。
$EXKMP$:有两个字符串$S,T$,要求输出$T$与$S$的每一个后缀的最长公共前缀

KMP

KMP算法的主要思想是：利用已经部分匹配这个有效信息，保持$S$指针不回溯，通过修改$T$指针，让模式串尽量地移动到有效的位置，重点就在于当某一个字符与主串不匹配时，我们应该知道$T$指针要移动到哪里。

首先

这里讲的字符串数组是从$[1,strlen(s)]$,并不是$[0,strlen(s))$
$next[i]$=字符串$[1,i]$之间相同的前后缀长度。这个数组是为$KMP$才出现的。

如果暴力匹配那么我们就要从$S[2]$开始继续判断是否匹配$T$。

而$KMP$

这个时候人们才想到去建造$Next$

求$next$

1
2
3
4
5
6
7
nxt[0] = -1; \\可以省去next[j]=(t[1]==t[j])(可以自行思考)
for (int i = 1, j; i <= m; i++)
{
    for (j = nxt[i - 1]; j >= 0 && b[j + 1] != b[i]; j = nxt[j])
        ;
    nxt[i] = j + 1;
}

匹配过程

1
2
3
4
5
6
7
8
9
10
for (int i = 1, j = 0; i <= n; i++)
 {
     for (; j >= 0 && b[j + 1] != a[i]; j = nxt[j])
         ;
     j++;\\准备下一次循环继续匹配
     if (j == m)
     {
         printf("%d\n", i - j + 1);
     }
 }

$Next$的数组的妙用

  • 求最小循环节 $xlen=i-next[i]$
  • 求最多循环次数 $xnum=i/xlen$

EXEMP

EXKMP算法的主要思想是：自己匹配一遍自己，再匹配文本串。

我们先定义一个：$extend[i]$表示$S[i…n]$与$T$的最长公共前缀长度，而题意就是让你求所有的$extend[i]$。

1
2
3
int pr = nxt[pl] + pl - 1;
int l2 = i - pl + 1;
int r2 = nxt[pl];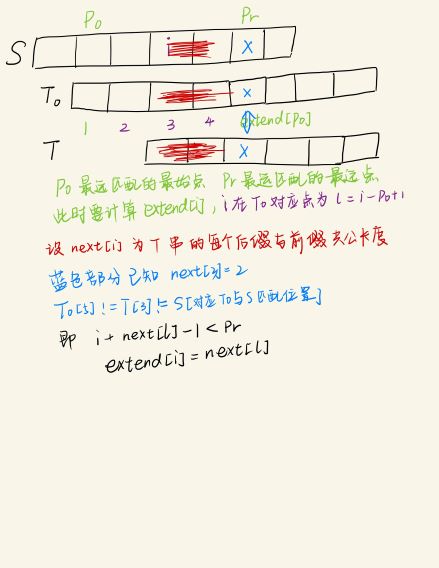

1
2
if (i + nxt[l2] - 1 < pr)
    nxt[i] = nxt[l2];

1
2
3
4
5
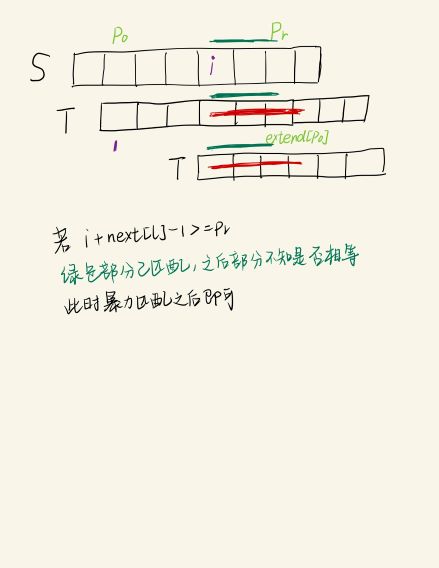
exlen = max(0, pr - i + 1);
while (exlen + i <= m && exlen + 1 <= m && t[exlen + i] == t[exlen + 1])
    exlen++;
nxt[i] = exlen;
pl = i;

而如何求这个$Next$数组

求$T$的每一个后缀与$T$的最长公共前缀长度

求$S$的每一个后缀与$T$的最长公共前缀长度

我们发现求$Next$的本质和求$Extend$一样

  • 注意求$Next$时我们要从第2位开始暴力，这样能防止求时引用自己$next$值的情况。